Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 바인딩
- 도커
- Bottom Up
- 자바
- 11724
- 링킹
- 연결요소
- 그래프
- 이분그래프
- DynamicProgramming
- JAVA_HOME
- 알고리즘
- n진법게임
- BFS
- 동적계획법
- 프로그래머스
- 완전이진트리
- dfs
- 1707
- 인오더
- 포화이진트리
- 포스트오더
- 9093
- 웹개발
- 순회
- Java
- 전공자따라잡기
- 백준
- 피보나치
- 이진트리
Archives
- Today
- Total
물음표 살인마
[DP] 피보나치 수열을 이용해 동적프로그래밍(Dynamic Programming) 이해하기 본문
안녕하세요 오늘은 알고리즘을 풀다보면 자연스럽게 만나게 되는 dp에 대해 알아보도록 하겠습니다.
DP, Dynamic Programming, 이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말합니다.
분할정복과 비슷하지만 분명한 차이점은 dp에서는 작은 문제들이 반복되며, 그것을 이용해 문제를 풀어나간다는 점입니다.
dp를 사용할 수 있는 가정은 두가지가 있습니다.
1. 큰 문제를 작은 문제로 분할 가능해야 하며,
2. 작은 문제에서 구한 정답이 그것을 포함하는 큰 문제에서도 동일해야 합니다.
그럼 본격적으로 피보나치 수열을 들여다보겠습니다.
저는 피보나치 수열의 26번째자리에 있는 값을 구하고 싶습니다.
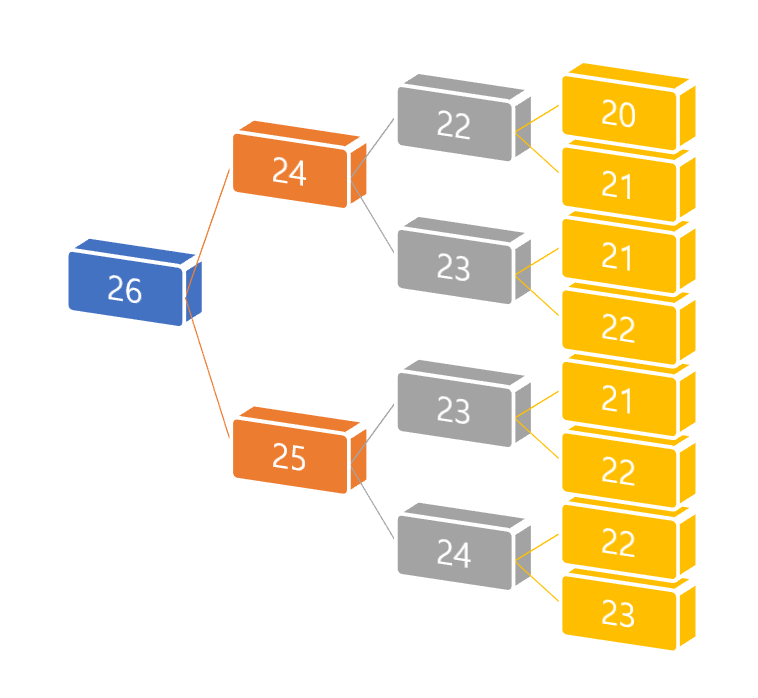
이는 dp[26]을 구하기 위한 극히 일부분만을 나타낸 그림임에도 불구하고
dp[22]의 값을 4번이나 계산해야 합니다.
위의 그림을 코드로 구현하면 다음과 같습니다.
public class Fibonacci01 {
public static void main(String[] args) {
System.out.println(recur(26));
}
public static int recur(int num){
if(num == 1){
return 1;
}
if(num == 2){
return 1;
}
int result = recur(num-1) + recur(num-2);
return result;
}
}
위의 알고리즘을 사용해 피보나치 수열을 계산하면 쓰이는 시간복잡도는 O(2^n)입니다.
26번째 수열은 금방 계산되지만 값을 조금만 높이면 한참동안의 시간이 걸립니다.
이것이 dp를 사용하는 이유입니다.
dp는 top-down 방식과 bottom-up 두 가지 방식으로 나뉘는데
top-down방식은 재귀함수를 사용하며 bottom-up은 반복문을 사용합니다.
1. 피보나치 수열 top-down
public class Fibonacci {
static int[] dp = new int[100];
public static void main(String[] args) {
System.out.println(fibo(26));
}
public static int fibo(int num){
//첫번재 수열인 경우
if(num == 1){
return 1;
}
//두번째 수열인 경우
if(num == 2){
return 1;
}
//배열에 저장된 값이 있을 시 저장된 값 반환
if(dp[num] != 0){
return dp[num];
}
//저장된 값이 없는 경우, 값을 저장 후 반환
return dp[num] = fibo(num-1) + fibo(num-2);
}
}2. 피보나치 수열 bottom-up
public class Fibonacci {
static int[] dp = new int[100];
public static void main(String[] args) {
System.out.println(fibo(26));
}
public static int fibo(int num){
//첫번째, 두번째 수열에 1 저장
dp[0] = 1;
dp[1] = 1;
//반복문을 돌며 3번째 수열부터 차례로 값을 채워넣는다
for(int i = 2; i < num; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[num - 1];
}
}
이렇게 동적 계획법을 사용하면 중복된 값을 두, 세번 계산할 필요 없게 되기 때문에
시간복잡도를 O(N)으로 줄일 수 있습니다.
'개발지식 > Algorithm' 카테고리의 다른 글
| [백준10845] 큐(queue)란? 자바로 큐 구현하기 (0) | 2022.08.22 |
|---|---|
| [백준9093] 단어뒤집기 세가지 방법으로 풀어보기 (0) | 2022.08.16 |
| [백준10828] 스택(stack)이란? 자바로 스택 구현하기 (0) | 2022.08.16 |
| 알고리즘 기초 (0) | 2022.08.15 |
| [백준1000] A+B : Scanner와 BufferedReader의 차이 (0) | 2021.07.18 |
Comments


